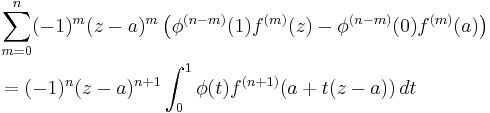Darboux's formula

Not to be confused with Christoffel–Darboux formula.

In mathematical analysis, Darboux's formula is a formula introduced by Gaston Darboux (1876) for summing infinite series by using integrals or evaluating integrals using infinite series. It is a generalization to the complex plane of the Euler–Maclaurin summation formula, which is used for similar purposes and derived in a similar manner (by repeated integration by parts of a particular choice of integrand). Darboux's formula can also be used to derive the Taylor series of the calculus.

Contents

Statement

If φ(t) is a polynomial of degree n and f an analytic function then

\begin{align} & \sum_{m=0}^n (-1)^{m}(z-a)^m\left(\phi^{(n-m)}(1)f^{(m)}(z) -\phi^{(n-m)}(0)f^{(m)}(a)\right) \\ & =(-1)^n(z-a)^{n%2B1}\int_0^1\phi(t)f^{(n%2B1)}(a%2Bt(z-a))\, dt \end{align}

The formula can be proved by repeated integration by parts.

Special cases

Taking φ to be a Bernoulli polynomial in Darboux's formula gives the Euler–Maclaurin summation formula. Taking φ to be (t − 1)n gives the formula for a Taylor series.

References

External links